|
The path becomes infinite. Here’s why:
|
We start with a path AD whose length we define as equal to 1.
|
 |
|
After the first substitution, the length is 4/3 because we’ve replaced the middle third with a piece twice its length, or 2/3 of the original path.
|
|
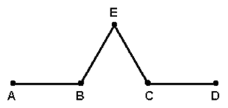
We can express the length of this new path as
1/3 + 1/3 + 1/3 + 1/3 = 4/3
with 1/3 referring to 1/3 of the original path.
|
 |
|
At the next step we replace each of the 1/3 pieces with a path that is 4/3 its length. For example, AB is replaced by a path that is 4/3 AB.
|
|
So the path is now 4/3 times what is was in step 2, which is
4/3 x 4/3 = 16/9
that is, 16/9 of the original path.
|
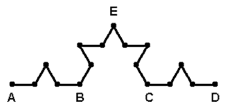 |
If we again replace each straight segment of the path with a path 4/3 its length, the length of the total path becomes
4/3 x 4/3 x 4/3 = 64/27
In general, if we carry out n replacements in a similar fashion, the length of the path is
4n / 3n
As n grows, 4n grows faster than 3n. As n approaches infinity, so does the length of the path.
This path is known as a Koch curve, named after Niels Fabian Helge von Koch (1870-1924) who invented it. It is an example of a fractal, a shape that looks the same at any scale—if you look at a tiny piece of the Koch curve under a microscope, it looks the same as the larger curve. If you increase the magnification, what you see still looks the same.
There are fractal patterns found in nature. If you look at cumulus clouds, for example, it is hard to tell if they are large and far away or small and close by. This is because they appear the same at any scale.
An interesting variant of the Koch curve is the Koch snowflake. Instead of starting with a straight line we start with an equilateral triangle. We perform the same replacements as we did before, but on each of the three sides of the triangle. The first three replacements look like this:
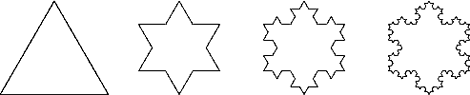
Now what does this have to do with the length of the coast of England? Benoit Mandelbrot, born in 1924, raised this question and found that it had no definite answer. It depends on how big your ruler is. If you measure the coastline with a 1 km ruler, you will be unable to follow small undulations of the coast. If you use a 1 m stick instead, you will be able to follow many small undulations that you missed with the 1 km ruler. Your measured path will be longer with the smaller ruler.

You will measure a longer path with the small red ruler than with the longer black ruler.
If you use a 1 cm ruler, you will follow even tinier variations and come up with an even longer result. There’s no finite limit, since you can, in principle, use smaller and smaller rulers, even to the point where you are measuring around the facets of the crystals of the rocks that make up the shore, or even the atoms that make up those crystals, or even . . .
The length of the coast of England is potentially infinite.
After we posted this puzzle, Claire Duffy asked if we meant the coast of England or the coast of Great Britain, including Scotland. Actually, it doesn’t matter, does it?
|